Probabilidad con la Distribución Normal

Escrito en 9 Abril, 2012 por Miguel

A partir de cualquier variable X que siga una distribución normal N(media, desv), se puede obtener una característica Z, que permite obtener y resolver preguntas de probabilidad acerca del comportamiento de variables que sigan aproximadamente este tipo de distribución.

Z = (X – Media) / Desv

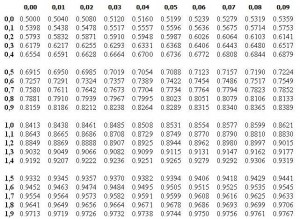
Esta propiedad es importante, ya que para una distribución N(0,1), existen tablas que nos permiten de manera fácil obtener la probabilidad de observar un dato menor o igual a un cierto valor Z.

Pongamos un ejemplo,

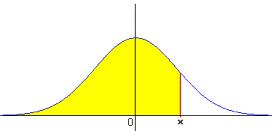
Imaginemos que los retornos anuales de un mercado cualquiera durante los últimos 25 años sigue una distribución aproximadamente Normal, con una media anual del 10% y una desviación estándar del 7%. ¿ Cuál es la probabilidad de que un año obtenido al azar tenga un retorno superior al 15% ?

N(10,7) X=15

Si la distribución fuera la de una Normal Estándar podríamos utilizar la tabla inferior, que calcula la probabilidad que nos interesa.

 

Aplicando la fórmula:

P(X=15) = (15 – 10) / 7 = 0,714 = P(Z=0,714)

Mirando en las tablas

P(Z=0,714) = 0,7611

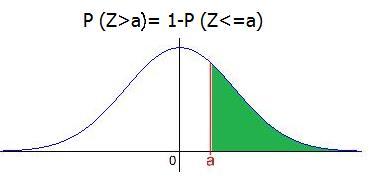
El área total bajo la curva es 1. Por lo tanto la probabilidad de que un año podemos alcanzar un retorno superior al 15% es de 1-0,7611= 0,2389. Es decir aprox. 23,89%.

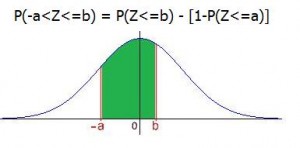
De la misma manera podemos obtener la probabilidad de obtener retornos anuales entre el 5% y el 15%.

 

 

---