La Distribución Normal

Escrito en 9 Abril, 2012 por Miguel

En todo proceso estadístico utilizamos una serie de medidas o valores para describir los datos con los cuales trabajamos. Estas medidas básicamente podemos dividirlas en medidas de posición y medidas de variabilidad.

Una medida de posición es aquel valor que se calcula para un grupo de datos y que se utiliza para describirlo de alguna manera o para destacar un valor típico dentro de un conjunto de datos. Entre las medidas de posición más empleadas encontramos por ejemplo la media aritmética, la mediana y la moda.

Una medida de variabilidad es aquel valor que se ocupa de describir la variabilidad (cambio) y su magnitud entre un conjunto de valores. Entre las más importantes destacan la desviación media, varianza, desviación estándar, coeficiente de variación y coeficiente de Pearson entre otras.

Una de las distribuciones teóricas más utilizada, es la distribución Normal o distribución Gaussiana. Esto es debido a la frecuencia con que algunos procesos habituales siguen de manera aproximada esta distribución. Esta familia de distribuciones con una forma común, están diferenciadas por su media y su varianza. La desviación estándar y la varianza están relacionadas entre si, de manera que la desviación estándar es la raíz cuadrada de la varianza. La Distribución Normal Estándar se corresponde a una distribución con media de 0 y varianza de 1 (N(0,1)).

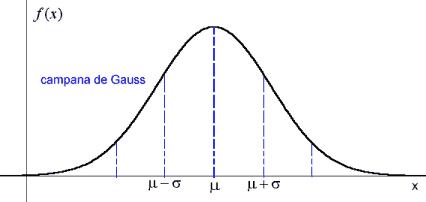
La desviación estándar es la medida de dispersión más importante, ya que se utiliza en muchos de los cálculos estadísticos habituales. Si consideramos que todo el conjunto de datos con los que trabajamos, pertenece a una distribución de frecuencias considerada como Normal (curva de frecuencias simétrica y mesokurtica, ni plana ni puntiaguda), entonces sabemos que el 68% de las mediciones se encuentran a no más de una desviación estándar de la media, y que aprox. el 95% de las mediciones se encuentra a no más de dos desviaciones estándar de la media.

La forma de la campana de Gauss depende de los parámetros media y desviación estándar. La media indica la posición de la campana, y la desviación estándar el grado de apuntamiento de la curva. A mayor desviación estándar, más dispersión de datos en torno a la media y más plana la curva. Con un valor más pequeño tenemos gran probabilidad de obtener datos más cercanos a la media de la distribución.

• Biografía
• Entradas recientes

Miguel

• Introducción al FOREX - 21 Enero, 2015
• Altman Z-Score - 20 Enero, 2015
• Alfa de Jensen - 27 Enero, 2014
• Benchmarks - 27 Enero, 2014
• VaR ( Value at Risk) - 26 Enero, 2014
• Cartera eficiente de Bolsia.com - 26 Enero, 2014
• Riesgo Sistemático - 23 Enero, 2014
• La Prima de Riesgo en el cálculo del Ke - 3 Diciembre, 2012
• Sortino Ratio (Ratios de Performance de Carteras) - 10 Noviembre, 2012
• Omega Ratio - 10 Noviembre, 2012

Ver todas las entradas